强化学习期末作业详解

本文是2022春季严瑞东老师《强化学习基础》期末作业的简要汇报

作业要求

本次作业包括三个部分：

1. 利用实时动态规划 (RTDP) 完成静态障碍物检测和路径的动态规划；
2. 利用S-T图撒点通过动态规划求速度曲线粗解；
3. 利用二次规划 (QP) 完成路径曲线和速度曲线的平滑。

整个的学习环境本来预定为由 PengZhenghao et al. 开源的 Metadrive 自动驾驶模拟器，但是由于使用较为复杂，而且本身对于控制方面的知识极为欠缺，所以老师允许我们自行编写环境。
环境总体要求：车道线 (Reference line) 在笛卡尔坐标系下是一条正弦曲线，振幅比波长尺度较小(即连续小弯路)，车道上有少数静态圆形障碍物，模拟小车近似为圆形。

背景知识简介

在汇报作业之前，先对一些必要的背景知识进行介绍。

Frenet坐标系

Frenet坐标系是自动驾驶领域为方便轨迹规划而引出的坐标系，即车辆坐标系。其两个坐标轴 S 轴和 L 轴 (或 D 轴) 正交，其中 S 轴表示平行于车道线的方向，即路径切向，L轴表示路径法向，所以其实Frenet坐标系就是车道线的自然坐标系。则 (s,l) 可用于描述车辆在道路中行驶了 s 的路程，车辆偏离中心线(即车道线) l 。这样转换坐标系后可将总问题变为三个子优化问题：一个横向优化、纵向优化和中线问题。从笛卡尔坐标系转换到Frenet坐标系可见文章

作业架构

主要分为四个部分，包括环境建构，路径规划，速度规划，可视化。一共六个 python 文件，分别实现如下功能：

roadenv.py

实现了道路环境类（roadEnv）的搭建，其中宏观路径的 reference_line 在笛卡尔坐标系下是 $y=\sin(0.02\pi * x)$ 的正弦曲线，车道宽2m。x 方向取了 0~100m 的距离，然后原本是打算利用随机设置障碍物加 dfs 搜索来制作障碍物的，但是由于容易出现障碍过多或过少的情况，所以最后从简，在 x=35m 和 x=75m 处设置了两个直径0.5m的圆形障碍。(小车直径为0.1m，不过好像代码中没有怎么体现出来💦)

原本是准备在frenet坐标系下划分栅格，然后计算 $(s，l) \to (s'，l')$ 的cost，但是这里设置的车道线是正弦函数，不利于获取 $x(s),y(s)$ 函数，(弧长积分是关于 $x$ 的第二类不完全椭圆积分)；又考虑到车道线近似于直线，于是在笛卡尔坐标系划分栅格设置了 $(x, y) \to (x', y')$ 的cost，这样规划出的路径误差不算太大。

cost：可参考此文，对于本环境中的cost设置如下式：

$cost = c_1 * \frac{1}{d_1}+c_2*d_2+c_3*|\delta\theta|$

其中 $c_i$ 为常数系数值，$d_1$ 为小车边界到障碍边界的距离 (这里其实可以略作变通，因为小车和障碍为了简化都变成了圆形，所以计算中心距离即可)，$d_2$ 为小车中心到 Reference line 的距离 (即L轴坐标值)，$|\delta\theta|$ 为航向角变化绝对值，这里解释一下，因为原本是打算在 frenet 坐标系划区进行动态规划，但是后来发现将 frenet 坐标变换到笛卡尔坐标有点困难，因为正弦函数的弧长积分是一个关于 $x$ 的第二类不完全椭圆积分，然后这样要求得 $x(s)$ 是比较困难的一件事，起码我现在想到的是计算一系列散点然后插值拟合曲线 (显然 $x(s)$ 是连续的)，所以本次就将问题简化，而在笛卡尔坐标下计算航向角变化也更加方便。由前面所述，这样造成的系统误差尚属可接受范围，起码在半定量的实验中可以接受。
然后还有一处是，最后的终点，原本应该是设置奖励值，但这里使用成本，也就是cost时就需要将这个“奖励”设为负数，即负成本。

rtdp.py

实现了利用rtdp（实时动态规划）在 roadEnv 环境中通过状态转移的 cost 求解最佳路径，基本思路就是利用贝尔曼最优方程，求解每一个状态的最优动作 (即最小化成本)，然后可以求解出一条路径粗解。
但是事实上，实现路径规划感觉用动态规划真的很少，像是RRT、A*、D*、Dijkstra这种算法明显用得更多吧💦，这样寻路真的计算量太大了吧……虽然用了rtdp不用对每一个状态的value进行更新，但是感觉依旧不值得这样算。可以参考酒井笃志先生的github仓库中pathplanning的一部分，然后还有一个用 JavaScript 写的一个模拟器可以用于辅助理解。

path_smooth.py

利用 scipy.interpolate 库中的 UnivariateSpline 样条插值法对曲线粗解进行平滑，也就是插值拟合曲线。选择这个方法的理由是，用plt打印出曲线粗解可以发现有部分噪声 (也许前面cost参数的设置不太理想)，然后在经过一系列插值法使用后，发现这个一元样条插值最好看 (所以如果要知晓原理逻辑推荐学习计算方法这门课)。下面是图示：

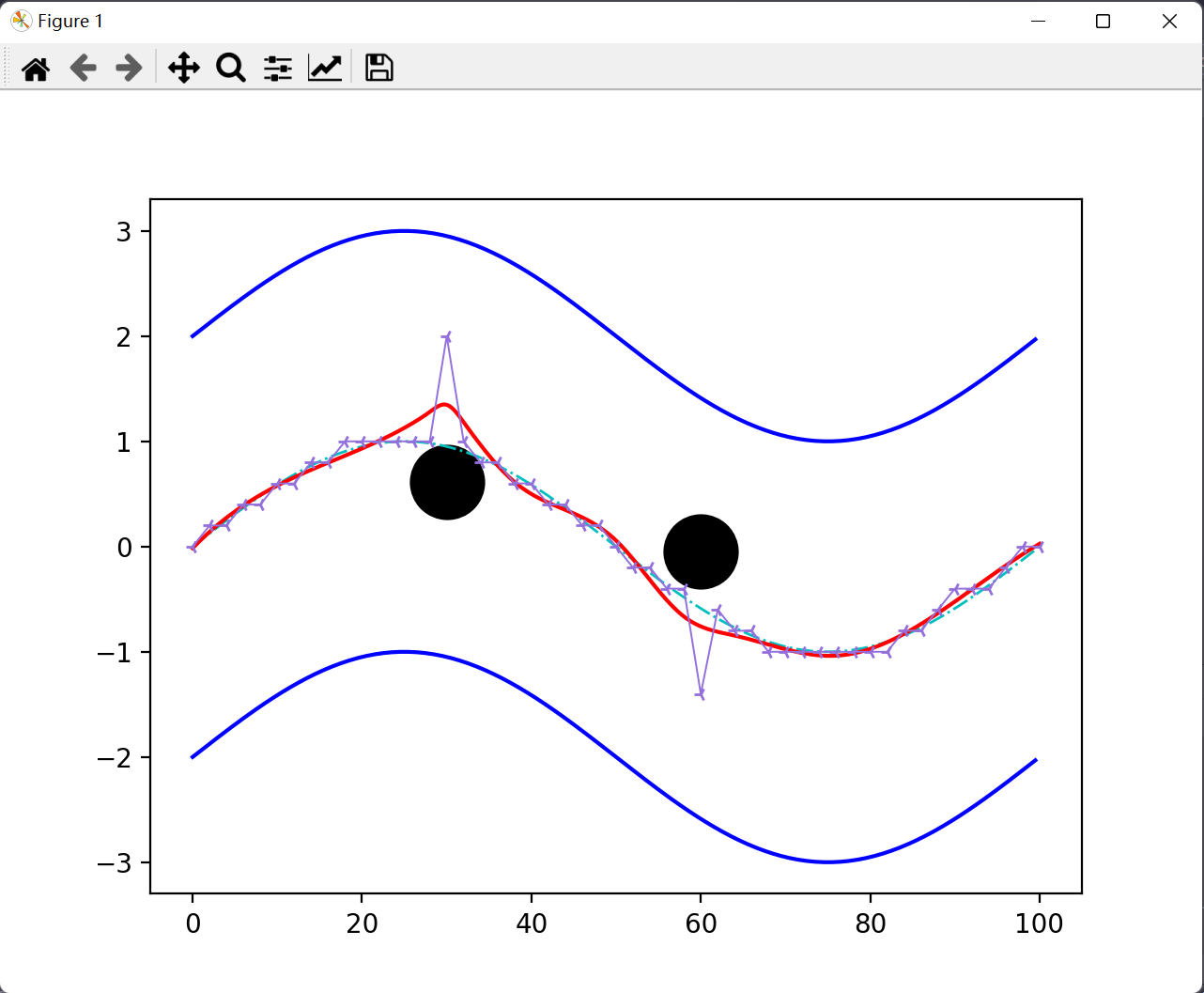
zuobiao.py

包含两个函数：
cartesian_to_frenet : 利用牛顿法迭代求解笛卡尔坐标系转换到frenet坐标系的值；
frenet_to_cartesian : 利用 pynverse 库中的 inversefunc 求解逆函数得到s对应的x值。
这里可以看出其实是可以得到坐标的转换的，但是我并不确定像是百度Apollo计划里是怎么做的，感觉应该和我这样粗暴且误差较大的求解差别甚大，所以再次强调本代码仅供参考，大部分逻辑经过了大刀阔斧的简化。

speed_planing

原本是包含了两个步骤：

1. 实现利用dp得到s-t图下的速度曲线粗解；
2. 实现利用五次多项式对速度曲线平滑，使速度、加速度和加加速度（jerk）值连续并稳定。
   但是！由于cost_table计算时参数设置遇到较大困难：

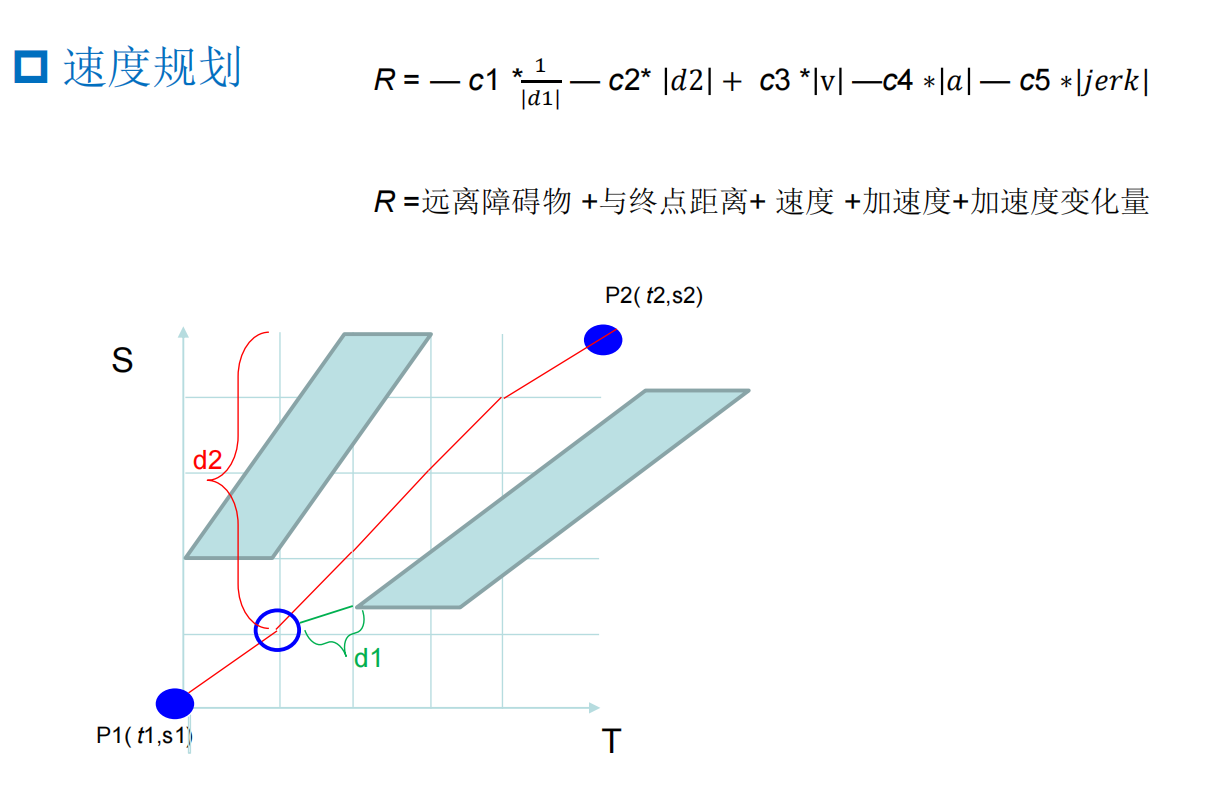
这里需要注意。由于我设置的是静态障碍物，所以实际上应该是一个平行于 t 轴的矩形，至于怎样理解和定义，可参考视频，然后其实这里的动态规划 (我的理解) 就是相当于写一个五重循环更新 dp 数组 (因为如果要求jerk值则需要取四个点，可参考文章)。然后这个 dp 数组就是相当于此文中的一个cost_table，当然也不大对，因为Apollo的代码用的是C++，利用了一些STL，所以可能具体实现不是这样的，不过总体的思路就是在S-T图上撒点动态规划求一个粗解。

但是这几个参数过于复杂，包括相关性、数量级都不是很清楚，想来可能需要一些车辆动力学的知识，遂选择手动估测曲线，取部分中间点代入步骤二得到速度规划，也就是一个平滑连续(且一二三阶导数均连续)的一个S-T曲线。

main.py

调用rtdp，path_smooth, speed_planing 文件获得最后的速度规划和路径规划结果，然后利用matplotlib.pyplot 库进行结果的可视化模拟，可视化模拟，由于取的是100米长(即一个周期)，然后平均速度大小约为10m/s，所以大概是12秒左右，以每0.1秒为1帧(SIMLOOP)，然后利用函数plt.cla和plt.gcf来绘制动图，至于怎么保存GIF图以及最后有一点点没能跑完整，我试图解决了一下，但是没有什么好的处理方法，加上作业ddl了，就大概水了上去。

代码在这里，演示视频在这里

总结

这个作业其实我的完成度相当低，但是收获蛮大的，譬如知道了大体逻辑，知道了什么用什么方法，然后亲自上手码代码也能体会到一个成熟的工程，对于系统架构的完整和可靠的严格要求，以及对算力的刚需。我虽然只是一个自动驾驶的小白，甚至现在还可以说是门外汉，但是能感受到其中庞大的知识体系，而且每一步都不只是自动驾驶，无人机、RPG游戏自动寻路、导航、轨迹追踪，无人机控制……也不只是强化学习，强化学习只是一种解决的思路。
如果有大佬发现我的错误或者知识误区，请不吝赐教。