计算思维第三次test题解及总结

  • 思路与AC代码
  • 总结

一、题解

A题

题意

给定一个正整数 xx，对数 xx 中的数位进行重排得到一个新数，求新数中大于原数的最小数。保证x不是最大的。
1≤x≤101001 \leq x \leq 10^{100}

思路

翻译一下就是找比 xx 字典序大的最小数，令 a[i]a[i] 表示 xx 的第i位数字 (从高位开始)，假设 a[i]a[i] 后的子串是降序排列的，而 a[i]a[i] 刚好破坏这种排列，而 a[j]a[j] 刚好是 a[i]a[i] 后的刚好比 a[i]a[i] 大的最小的数，找到这两个数并交换，然后对i位之后的数升序排列即为答案。
例子：对于1938762，则交换3与6，得到1968732，将8732升序排列得到2378然后拼起来得到1962378即为答案。
注意 xx 的范围包含了个位数，说明对于1到9直接输出原数即可

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
void solve(string s)
{
    int len = s.size(), a, b;
    if(len==1)
    {
        cout << s << endl;
        return;
    }
    //寻找i
    for (int i = len - 1; i > 0;)
    {
        if(s[i-1]>=s[i])
            i--;
        else
        {
            a = i - 1;
            break;
        }
    }
    //寻找j
    for (int j = len-1; j>a;)
    {
        if(s[j]<=s[a])
            j--;
        else 
        {
            b = j;
            break;
        }
    }
    //交换然后排序
    swap(s[a], s[b]);
    sort(s.begin() + a + 1, s.end());
    cout << s << endl;
}
void swap(char &a,char &b)
{
    char tmp = a;
    a = b;
    b = tmp;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    string s;
    cin >> s;
    solve(s);
    return 0;
}

B题

题意

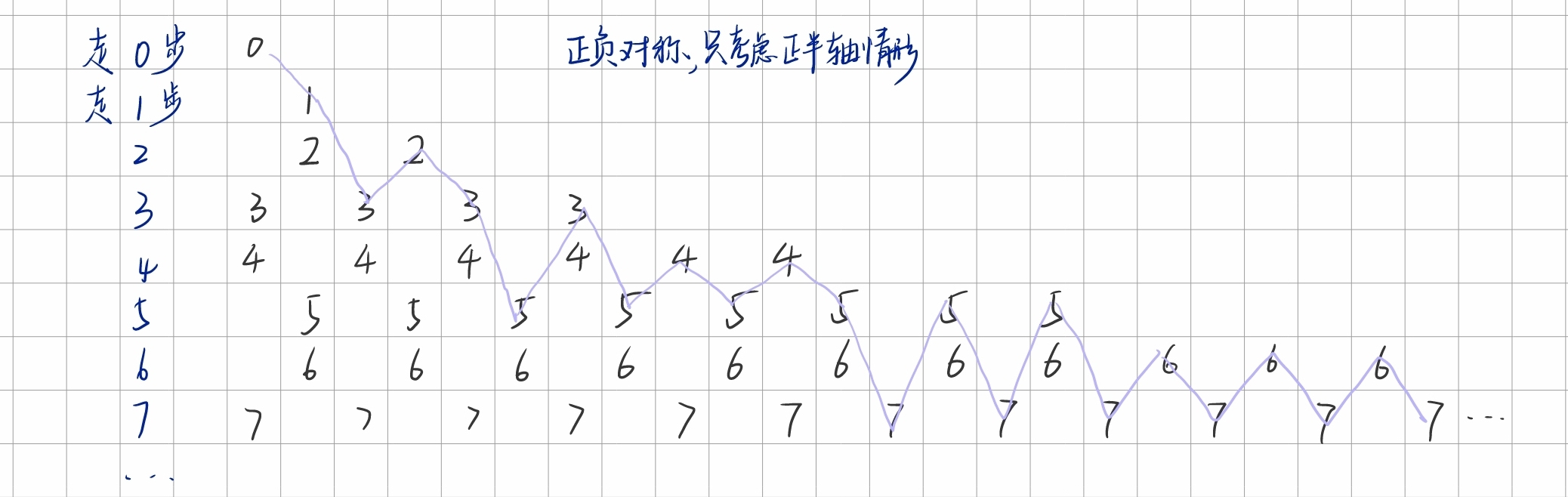
初始位置为0，初始步长为1，每次可以向左或者向右跳(一维运动)，每跳一次步长增加1，求到达坐标 xx 的最短步数。一共 qq 次询问
1≤q≤106,−109≤x≤1091 \leq q\leq 10^6,-10^9\leq x\leq 10^9

思路

由于询问次数就是1e6的数量级，说明每次查询都是 O(1)O(1) 的复杂度。那么真相只有一个，就是找规律()
由此我们画画图可以轻松看出来规律：
找规律
即走 ii 步的边界坐标是 ai=(i+1)∗i2a_i=\frac{(i+1)*i}{2}，那么：

  • 如果刚好 ai=xa_i=x，则到达 xx 的最短步数为 ii；
  • 如果 ai<x<ai+1a_i<x<a_{i+1} 且 ii 为奇数，那么 x−aix-a_i 为奇数时步数为 i+2i+2，为偶数时步数为 i+1i+1；
  • 如果 ai<x<ai+1a_i<x<a_{i+1} 且 ii 为偶数，那么 x−aix-a_i 为奇数时步数为 i+1i+1，为偶数时步数为 i+3i+3；

有点丑的规律，或许有大佬给一个美观的证明或者美观的形式？
其次需要考虑一个问题，怎么求 ii ?
如果每次都用for循环，毫无疑问可能超时 ( O(qx)O(q\sqrt{x}) 的复杂度 )，那么这里选择存一个预处理好的表，毫无疑问是单增的，然后对于每次查询二分查找就行了。( O(q+x)O(q+\sqrt{x}) 的复杂度 )

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
int pre[45000];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int q, x;
    cin >> q;
    FORU(i,0,45000)
        pre[i] = i * (i + 1) / 2;
    while(q--)
    {
        cin >> x;
        if(x==0)
        {
            cout << 0 << endl;
            continue;
        }
        else if(x<0)
            x = -x;
        int i,ans;
        i = upper_bound(pre, pre + 45000, x) - pre - 1;
        int a = pre[i];
        if(i&1)
        {
            if(x==a)
                ans = i;
            else
            {
                if((x-a)&1)
                    ans = i + 2;
                else
                    ans = i + 1;
            }
        }
        else
        {
            if(x==a)
                ans = i;
            else
            {
                if((x-a)&1)
                    ans = i + 1;
                else
                    ans = i + 3;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

C题

💦题跳过

D题

题意

有 nn 种物品，第 ii 种物品个数为 w[i]w[i]，单价为 v[i]v[i]。可选择一个区间进行单价的反转，即将区间中第一种和最后一种物品的单价对调，第二种和倒数第二种物品的单价对调，依此类推，求反转一个区间后的总价值最大值。
1≤n≤5×103,1<vi,wi<1031\leq n \leq 5 \times 10^3 , 1 < v_i,w_i < 10^3

思路

显然直接暴力是 O(n3)O(n^3) 的复杂度，那么考虑用数组 f[i][j]f[i][j] 表示从 ii 到 jj 进行反转后与原来的差值，那么有

f[i][j]=f[i+1][j−1]+v[i]∗w[j]+v[j]∗w[i]−v[i]∗w[i]−v[j]∗w[j]\footnotesize f[i][j] = f[i+1][j-1] + v[i]*w[j] + v[j]*w[i] - v[i]*w[i] - v[j]*w[j]

加上原价值就好了，

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
int pre[5010][5010];
int v[5010], w[5010];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    FORU(i,1,n)
    {
        cin >> v[i];
    }
    FORU(i,1,n)
    {
        cin >> w[i];
    }
    FORU(i,1,n-1)
    {
        FORU(j,1,n-i)
        {
            pre[j][i + j] = pre[j + 1][i + j - 1] + v[j] * w[i + j] + v[i + j] * w[j] - v[j] * w[j] - v[i + j] * w[i + j];
        }
    }
    int diff = 0;
    FORU(i,1,n)
    {
        FORU(j,i,n)
        {
            diff = max(pre[i][j], diff);
        }
    }
    FORU(i,1,n)
    {
        diff += v[i] * w[i];
    }
    cout << diff << endl;
    return 0;
}

E题

题意

给定一个序列 ( 长度为 nn )和一个整数 kk，从中选择两个无交集的连续子序列，使得每个子序列中所有元素的和正好等于所给的整数 kk。给出满足条件的两个子序列最小长度和，如果不存在满足条件的子序列，则输出 −1-1。
1≤n≤106,1≤k≤1081 \leq n \leq 10^6 , 1 \leq k \leq 10^8，序列中 1≤ai≤1031\leq a_i\leq 10^3

思路

前缀和然后查找记录所有合理的子序列，然后遍历每个子序列，找除去该子序列的剩下的子序列中最短的，加起来然后更新最短两个和的值。
第一步是记录所有子序列，即使用了前缀和，如果正常暴力找也是 O(n2)O(n^2) 的复杂度，于是发现前缀和必是单增的数组，如果子序列以 aia_i 结尾，只需要用二分查找以前 i−1i-1 位中某数为子序列开头的位置即可，然后可记录下所有合理子序列的开头 fromfrom、末尾 toto
第二步，假设找到的子序列共 mm 个，那么 0≤m≤n0\leq m\leq n。我们发现如果暴力遍历每个子序列 ( 长度为 len1len1 )，查找剩下子序列中不与该序列重叠的最短值 ( 长度为 len2len2 )，复杂度是 O(n2)O(n^2) ，又超时了😭。
那么这个时候选择一种巧妙的贪心思路，假如我知道每个 len1len1 对应的 len2len2 值是不是就简单了，那么就做一个预处理。即我事先记录下了每个子序列的开头和结尾，那么用一个数组 len[i]len[i] 表示第 ii 位之后 ( 含第 ii 位 ) 的原序列中合理子序列的最短值，如果没有合理子序列就将该值赋为 nn。
那么对于第 ii 个最短子序列，开头为 from[i]from[i]，末尾为 to[i]to[i]，所求值:

ans=min⁡i ( len[ to[i]+1 ]+to[i]−from[i]+1 )ans=\min_i\ (\ len[\,to[i] + 1\,] + to[i] - from[i] + 1\,)

至于如何预处理这个 len[i]len[i] 数组，就是先都取一个数比如 nn ,从后往前遍历，遇到更短的就更新即可，是一个贪心地思想，如果讲得不明白可以看看代码然后把每个 len[i]len[i] 打印出来看看。这样查询最短两个的和的复杂度就压缩到了 O(n)O(n)。总体复杂度是 O(nlogn)O(nlogn)

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
const int N = 1e6;
int len[N + 5], qz[N + 5];
vector<int> from, to;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n, k, a;
    cin >> n >> k;
    FORU(i, 1, n)
    {
        cin >> a;
        qz[i] = qz[i - 1] + a;
        len[i] = n;
    }
    FORU(i, 1, n)
    {
        int j = lower_bound(qz, qz + i, qz[i] - k) - qz;
        if (qz[j] == qz[i] - k)
        {
            from.push_back(j + 1);
            to.push_back(i);
            len[j + 1] = i - j;
        }
    }
    int sublen = len[n];
    for (int i = n; i > 0; i--)
    {
        sublen = min(sublen, len[i]);
        len[i] = sublen;
    }
    int totlen = INT_MAX, group = from.size();
    FORU(i, 0, group - 1)
    {
        if (len[to[i] + 1] == n || to[i] == n)
            continue;
        totlen = min(len[to[i] + 1] + to[i] - from[i] + 1, totlen);
    }
    if (totlen == INT_MAX)
        cout << -1;
    else
        cout << totlen;
    return 0;
}

附：这里斗胆放上大佬的滑动窗口代码，思路就不讲解了，有兴趣可以看看，时间复杂度一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;

const int M = 1e6;
int nums[M + 1];
int len[M + 1];
int lft[M + 1];
int main() {
	int n;
	long long k;
	cin >> n >> k;
	for(int i = 0; i < n; i++) {
		scanf("%d", nums + i);
		lft[i] = n;
		len[i] = n;
	}
	int l = 0, r = 0;
	long long cur = 0;
	for(; r < n && cur < k; cur += nums[r], r++);
	if(cur == k) {
		lft[l] = min(lft[l], r);
		len[l] = min(len[l], r - l);
		cur += nums[r++];
	}
	while(r < n) {
		for(; cur > k; cur -= nums[l++]);
		if(cur == k) {
			lft[l] = min(lft[l], r);
			len[l] = min(len[l], r - l);
			cur -= nums[l++];
		}
		for(; r < n && cur < k; cur += nums[r++]);
		if(cur == k) {
			lft[l] = min(lft[l], r);
			len[l] = min(len[l], r - l);
			cur += nums[r++];
		}
	}
	int ans = INT_MAX;
	int mn = len[n - 1];
	for(int i = n - 1; i > -1; i--) {
		mn = min(mn, len[i]);
		len[i] = mn;
	}
//	for(int i = 0; i < n; i++) cout << lft[i] << ' ';
	for(int i = 0; i < n; i++) {
		if(lft[i] == n) continue;
		if(len[lft[i]] == n) continue;
		ans = min(ans, lft[i] - i + len[lft[i]]);
	}
	if(ans == INT_MAX) cout << -1;
	else cout << ans;
	return 0;
}

F题

老实说也挺水的，放以前我就写了，不过最近作业太多加上期末月，挺寄的，请原谅我的偷懒，就给大家送上一只小鹿乃好了()

二、总结

  • 大创折磨人，程设折磨死人，要不是github有一点答案抄，我可能寄了，大概暑假我也会把我的答案传上去，希望学弟学妹不受这个折磨，md
  • 太忙啦太忙啦我要崩溃了呜呜呜
#算法
计算思维第三次test题解及总结
https://zongjy.github.io/2022/05/18/6478b71fe701/
作者
zongjy
发布于
2022年5月18日
许可协议