数据结构复习

说是复习，不如说是预习😕

基础

1. 组成数据的基本单位是数据元素，最小单位是数据项
2. 逻辑结构分为线性结构（线性表）和非线性结构（集合、树形结构、图状结构）
3. 存储结构分为顺序存储（数组）、链式存储（单链表）、索引存储（索引表）、哈希存储（哈希表）

二分查找

int binary_Search(const int *array, int end, int start, int key)
{
	int left, right, mid;
	left = start, right = start;
	while(left <= right)
	{
		mid = left + (right - left)/2; // 防止溢出
		if(array[mid] == key) return mid;
		else if(array[mid] < key) right = mid - 1;
		else if(array[mid] > key) left = mid + 1;
	}
	return -1;
}

链表

1. 单链表不是随机存储结构
2. 循环链表中，任一结点的前驱指针均不为空

判断单链表中心对称

快慢指针找到中间结点，然后翻转后半链表再进行比较判断

int is_center_symmetric(Node *head)
{
	Node *slow, *fast;
	slow = fast = head;
	
	while(fast != NULL && fast->next != NULL)
	{
		slow = slow->next;
		fast = fast->next->next;
	}
	// 总结点数为奇数时跳过中间（slow指向后半部分第一个结点）
	if(fast != NULL)
		slow = slow->next;
	
	// 翻转后半部分链表
	Node *prev, *curr;
	prev = NULL, curr = slow;
	while(curr != NULL)
	{
		Node *next = curr->next;
		curr->next = prev;
		prev = curr;
		curr = next;
	}

	// 比较并判断
	Node *first, *second;
	first = head, second = prev;
	while(second != NULL)
	{
		if(first->data != second->data)
			return 0;
		first = first->next;
		second = second->next;
	}
	return 1;
}

串

kmp匹配算法

kmp 的精髓是 next 函数（以及其改良后的 nextval 函数）

算出来的 next 数组意义在于：主串与模式串失配时，模式串回溯的位置（主串不用回溯）

下面是计算 next 数组的方法：

$\small next[j] = \begin{cases} 0 & j=1 时 \\ \max\{k|1<k<j,且p_1\ldots{}p_{k-1} = p_{j-k+1}\ldots{}p_{j}\} & 集合不为空时 \\ 1 & 其他情况 \end{cases}$

用人话讲就是 $ next[1]=0 $，然后 $next[j]$ 就是模式串的前 $j-1$ 个字符的前后缀匹配的最大长度加1，例如aaaba的前后缀匹配最大长度就是1

nextval 数组主要解决模式串中有大量连续重复的字符时的问题：

$\small nextval[j] = \begin{cases} next[next[j]] & p_j = p_{next[j]}时 \\ next[j] & p_j \not ={} p_{next[j]}时 \end{cases}$

下面是一些示例代码：

void getNext(string T,int *next) 
{
	int i = 1, j = 0;
	next[1] = 0;
	while(i < T.length()) 
    {
		if(j == 0 || T[i] == T[j]) 
        { 
            //相等时，next的值等于j+1
			++i;
			++j;
			next[i] = j;
		} 
        else 
        {
			j = next[j];//往前寻找更小的匹配的子串
		}
	}
}

void getNextVal(string T, int *nextval)
{
	int i = 1, j = 0;
	nextval[1] = 0;
	while(i < T.length()) 
    {
		if(j == 0 || T[i] == T[j]) 
        { 
            //相等时，next的值等于j+1
			++i;
			++j;
            if(T[i] != T[j])
			    nextval[i] = j;
            else
                nextval[i] = nextval[j];
		} 
        else 
        {
			j = nextval[j];//往前寻找更小的匹配的子串
		}
	}
}

// 例如模式串是abaabcac
// next = 01122312
// nextval = 01021302

数组

栈

有一种东西叫做共享栈，两个顺序栈共享一个一维数组空间，栈底分别设置在两端，向中间延伸。有以下特点：

• 两个栈的栈顶指针都指向栈顶元素，$top_0=-1$ 时 $0$ 号栈为空，$top_1=MaxSize$ 时 $1$ 号栈为空。
• 当两个栈顶指针相邻时， $top_1-top_0=1$ ，判断为栈满。
• 当 $0$ 号栈进栈时 $top_0$ 先加 $1$ 再赋值，$1$ 号栈进栈时 $top_1$ 先减 $1$ 再赋值，出栈时则刚好相反。
• 存取数据的时间复杂度均为 $O(1)$。

广义表

1. 一个广义表中的元素分为原子元素和子表元素两类
2. tail：删去表中第一个元素，head：取第一个元素

哈希

1. 为了有效利用hash查找技术，必须解决的两个问题是构建好的hash函数、确定解决冲突的方法

树

1. 引入二叉搜索树的目的是加快查找结点的前驱或后继的速度
2. 二叉树有5种基本形态
3. 令二叉树中度为0的节点数为 $N_0$，度为1的为 $N_1$，度为2的为 $N_2$（也即叶子结点数），存在等式 $N_0+N_1+N_2=N_1+2*N_2+1$

二叉排序树

向二叉排序树插入新节点的时间复杂度：介于 $O(n)$ 和 $O(\log_{2}n)$ 之间

判断二叉排序树

判断二叉树是否为二叉排序树的一个思路是：如果中序遍历二叉树得到的序列是升序的，那么该二叉树是二叉排序树

int is_BSTree(Node *root)
{
	static Node *prev = NULL;
	if(root)
	{
		if(is_BSTree(root->left))
			return false;
		if(prev != NULL && root->data <= prev->data)
			return false;
		prev = root;
		return is_BSTree(root->right)
	}
	return true;
}

哈夫曼树

哈夫曼树没有度为1的节点

哈夫曼树的构造方法如下：

1. 将权值集合中的所有权值构造成叶子节点
2. 每次从权值集合中选取两个最小的权值，构造一个新的父节点，并将这两个最小权值对应的叶子节点作为新父节点的左右子节点
3. 重复步骤2直到只剩下一个节点，这就是哈夫曼树的根节点

可参考这篇文章

图

1. 对于具有 $n$ 个顶点和 $e$ 条边的无向图，邻接表中需要构建 $n$ 个首元结点和 $2e$ 个表示边的结点；对于具有 $n$ 个顶点和 $e$ 条弧的有向图，邻接表需要构建 $n$ 个首元结点和 $e$ 个表示弧的结点。
2. 有向图邻接矩阵中，第 $i$ 行的所有非零元素个数为顶点 $i$ 出度（列入行出）
3. 强连通图指从任意一个点到另一个点都有路径，对于有 $n$ 个顶点的强连通图，最少有 $n$ 条边，最多有 $n(n-1)$ 条边
4. 在图的邻接表中用顺序存储结构存储表头节点的优点是可以随机访问到任一个顶点的简单链表

拓扑排序

对于一个有向无环图，对所有的节点进行排序，要求没有一个节点指向它前面的节点。

1. 先统计所有节点的入度，对于入度为 $0$ 的节点就可以分离出来，然后把这个节点指向的节点的入度减一。
2. 重复步骤一，直到所有的节点都被分离出来。
3. 如果最后不存在入度为 $0$ 的节点，那就说明有环，不存在拓扑排序

最小生成树

Prim 算法

1. 选取权值最小边的其中一个顶点作为起始点。
2. 找到离当前已选择顶点权值最小的边，并记录该边连接的新顶点为已选择。
3. 重复第二步，直到找到所有顶点，就找到了图的最小生成树。

Kruskal 算法

1. 将图中的所有边都去掉。
2. 将边按权值从小到大的顺序添加到图中，并保证添加的过程中不会形成环。
3. 重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

排序

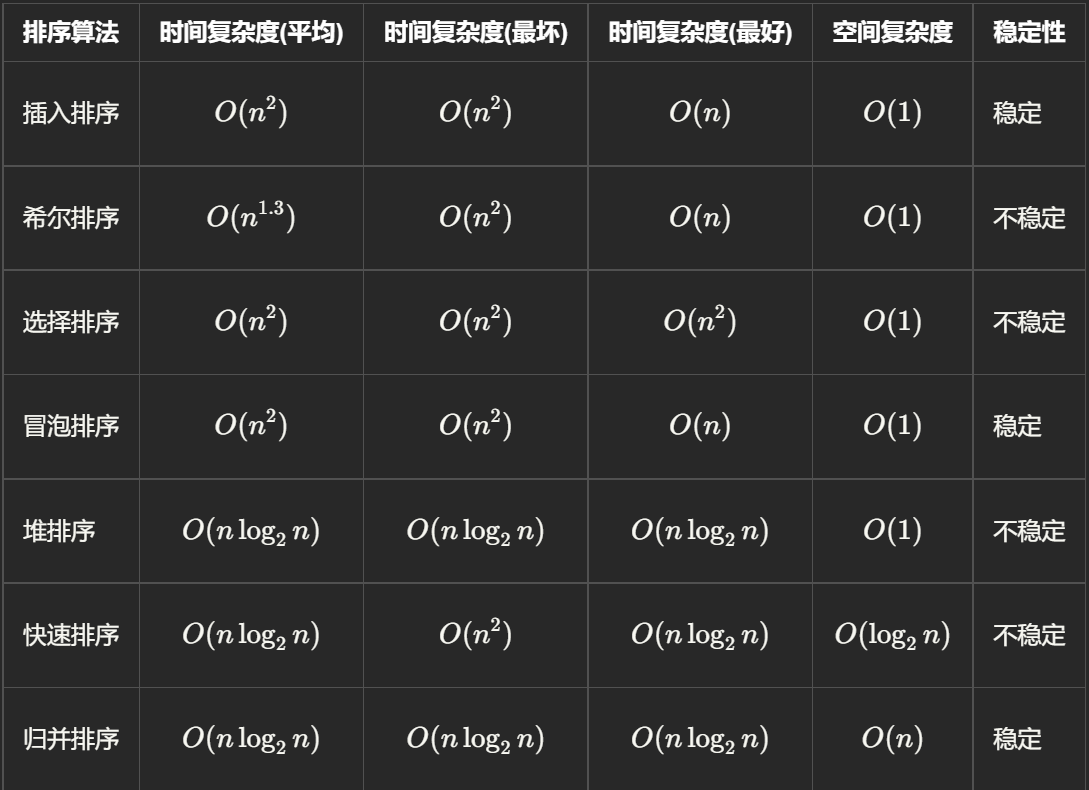
选择排序 & 插入排序

选择排序：从前向后寻找最小值，然后将最小值与首部交换，然后首部向后移动1位，重复此过程

插入排序：第 $i$ 趟选择 $arr[i]$ 为key，然后从第 $i$ 位向前找第一个比key小的数，将 $arr[i]$ 插到这里，后面的向后覆盖。

快速排序

一般考的是填坑法，可以参考这里

这里给一个例题：

Q：设一组初始记录关键字序列为 $(19,21,16,5,18,23)$ ，要求给出以 $19$ 为基准的一趟快速排序结果。

A：$(18,5,16,19,21,23)$

堆排序

建立初始堆有两种方法，向上筛选法，向下插入法，没说都是小根堆

堆排序中需要1个辅助记录单元