计算思维第二次test题解及总结

  • 思路与AC代码
  • 总结

一、题解

A题

题意

每次操作能自由交换两个元素，求把一个方阵转置的最小操作次数。

思路

一开始以为是固定的，直接计算右上三角形 n(n−1)2\frac{n(n-1)}{2} 即可，后来一看样例，原来是只需要满足是转置的就够了，所以对于方阵 AA 和操作后的 A′A^{'}，只需要做到 Aij=Aji′A_{ij}=A_{ji}^{'} 即可。那么我们对于右上三角形，只要发现是和对角线对称的元素相等就不用操作这一对数，减去这些不用操作的就是答案。(1≤n≤800)(1\le n\le 800)

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m;++i)
#define endl '\n'
typedef long long ll;
int a[1005][1005];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,tmp,res=0;
    cin >> n;
    FORU(i,1,n)
    {
        FORU(j, 1, n)
        cin >> a[i][j];
    }
    if(n==1)
        cout << 0;
    else
    {
        FORU(i,2,n)
        {
            FORU(j, 1, i-1)
            {
                if(a[i][j]==a[j][i])
                    res--;  //减去不需要的
            }
        }
        res += (n * (n - 1)) / 2;//总操作数
        cout << res;
    }
    return 0;
}

B题

题意

给定一个小数 dd 和整数 nn，在分母不超过给定整数 nn 的条件下，求数值上最接近给定小数 dd 的最简分数。
如果这个数为整数，则输出整数。并输出两者绝对值之差(保留十位小数)，如果答案不止一种则输出 “More than one!”（不包括引号）。
整数nn满足 1≤n≤1061\le n\le 10^6，小数 dd 满足 1≤d≤1001\le d\le 100，且保证 dd 的小数位数不超过 10 位。

思路

  1. 先判断 dd 是不是整数，是整数直接输出该整数和0.0000000000；
  2. 遍历分母，然后计算分母与小数的乘积得到一个浮点数，然后将这个浮点数四舍五入得到一个整数作为分子。再将这个分子除以分母得到这个分数的小数形式(转为double类型再除)，然后计算误差值，并更新最小误差和对应的分子分母。
  3. 最后判定这个误差乘以分母是不是 0.5，如果是说明分子减去1也是一个合理解(即误差一样)，那么输出 “More than one!”（不包括引号）
  4. (补充)我只能说有点好笑，我想反推一下它的测试数据有多少个是 “More than one!”情况的，结果当我注释掉那一段判定再提交时发现也是对的……这个数据也太水了😅

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
void solve(int n,double d)
{
    int td = (int)d;
    if((double)td==d)
    {
        cout << td << ' ' << 0.0;
        return;
    }
    int mfenzi = 1, mfenmu = 1;
    double eps = 7777.7777;  //lucky number 7!
    bool flag = false;
    FORU(i,1,n)
    {
        int fenzi = (int)(i * d + 0.5);
        double teps = abs((double)fenzi / i - d);
        if(teps<eps)
        {
            eps = teps;
            mfenzi = fenzi;
            mfenmu = i;
            flag = true;
            continue;
        }
    }
    if(eps*mfenmu==0.5)
    {
        cout << "More than one!";
        return;
    }
    cout << mfenzi << "/" << mfenmu << " " << eps;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    double d;
    cin >> n;
    cin >> d;
    //设置10位小数，当然用printf也是可以的
    cout.setf(ios::fixed);
    cout << setprecision(10);
    solve(n, d);
    return 0;
}

C题

题意

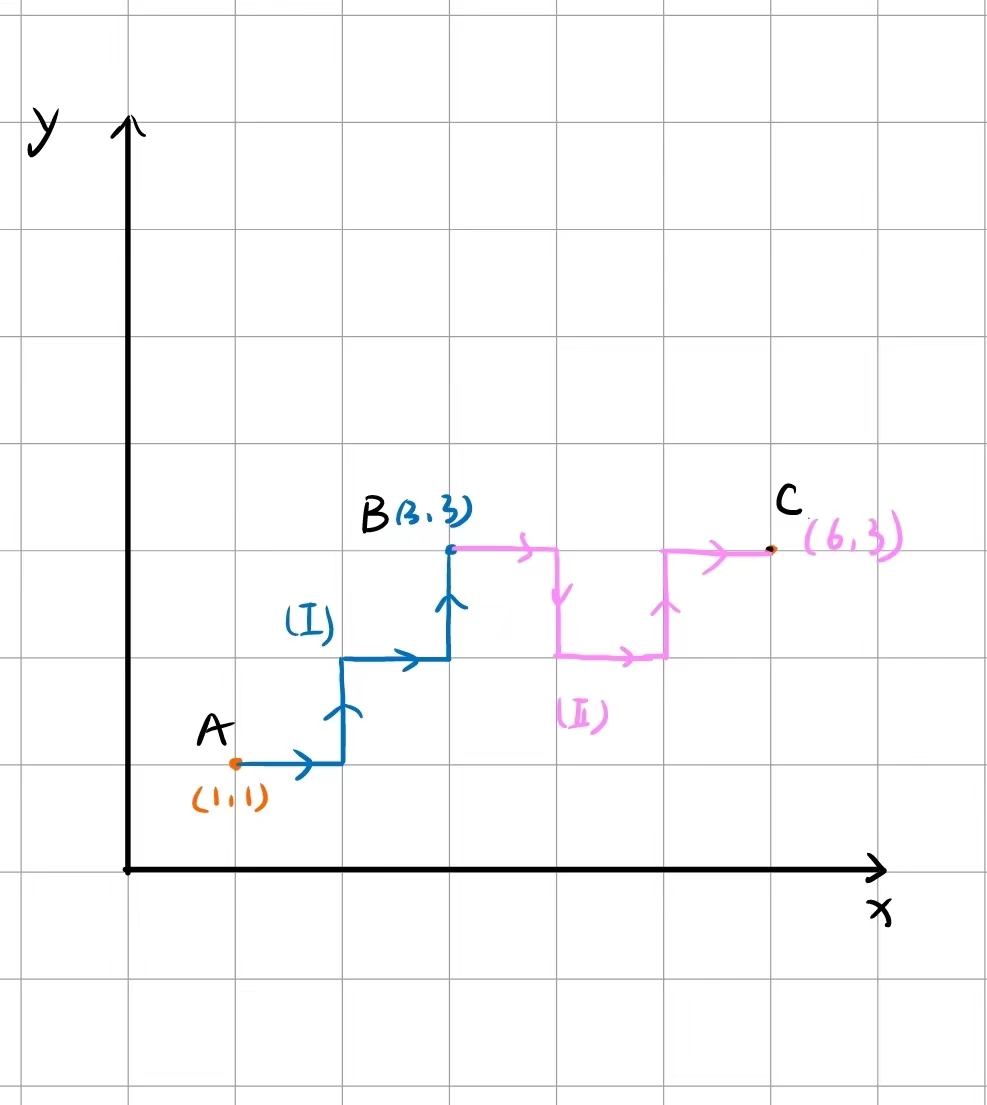
从点 (xs,ys)(x_s,y_s) 走到 (xt,yt)(x_t,y_t) 点 (均是整数), 每步能走一个单位长度, 只能沿平行于坐标轴的方向运动, 每走一步需要向左或向右旋转 90°, 求最少需要走多少步du。
所有坐标满足 −10000≤x,y≤10000-10000\le x,y\le 10000.

思路

  1. 首先注意到每走一步都要转弯，那么可以考虑先走类倾斜角为45°的折线，然后走到一个点 (x,y)(x,y)，并且该点与终点连线平行于坐标轴。即x=xtx=x_t或者 y=yty=y_t。
  2. 然后现在在同一直线上，两点距离设为 dd ，如果 dd 是奇数，则还需要走 (2∗d−1)(2*d-1) 步；如果是偶数，则还需要走 (2∗d)(2*d) 步。

示例
上图是一个示例，可以结合理解。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m;++i)
#define endl '\n'
typedef long long ll;
int a[1005][1005];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int x1, y1, x2, y2, res = 0;
    cin >> x1 >> y1 >> x2 >> y2;
    int dx = abs(x1 - x2);
    int dy = abs(y1 - y2);
    int mind = min(dx, dy);
    int rem = max(dx, dy) - mind;
    if(rem&1)
        res = 2 * rem - 1 + 2 * mind;
    else
        res = 2 * (rem + mind);
    cout << res;
    return 0;
}

D题

题意

给定一组整数数列 a1,a2,…,ana_1,a_2,\dots,a_n，求该数列中所有子区间的积为负数、0 和正数的个数。其中，子区间 [l,r][l,r] 的积定义为 ∏i=lrai\prod ^r_{i=l}a_i。
且满足 1≤n≤1051\le n\le 10^5，∣ai∣≤109|a_i|\le 10^9.

错误思路

一开始想的是用前缀和，数组 fs[i]fs[i] 存取前 ii 个数的负数个数，以及 zero[i]zero[i] 存取前 ii 个数的零的个数，然后对于每个区间进行查询，判断这个区间是正的，负的还是零，然后累加即可，非常暴力的想法，毫无疑问在查询累加这一段的时间复杂度是 O(n2)O(n^2) 的，那么这个题显而易见就 TLE 了，所以需要另寻出路。

正确思路

考虑用 zs[i],fs[i],zero[i]zs[i], fs[i], zero[i] 分别表示以 aia_i 结尾的且积为正数、负数、零的子序列个数，那么显然有递推式：

zs[i+1]={zs[i]+1if a[i+1]>0fs[i]if a[i+1]<00if a[i+1]=0(1)zs[i+1]= \begin{cases} zs[i]+1 & if\,a[i+1]>0 \\ fs[i] & if\,a[i+1]<0 \\ 0 & if\,a[i+1]=0 \end{cases}\tag{1}

fs[i+1]={fs[i]if a[i+1]>0zs[i]+1if a[i+1]<00if a[i+1]=0(2)fs[i+1]= \begin{cases} fs[i] & if\,a[i+1]>0 \\ zs[i]+1 & if\,a[i+1]<0 \\ 0 & if\,a[i+1]=0 \end{cases}\tag{2}

zero[i+1]={zero[i]if a[i+1]≠0 zero[i]+zs[i]+fs[i]+1if a[i+1]=0(3)\small zero[i+1]= \begin{cases} zero[i] & if\,a[i+1]\neq0\, \\ zero[i]+zs[i]+fs[i]+1 & if\,a[i+1]=0 \end{cases}\tag{3}

那么最后在从 1 到 n 求和即为答案。
而这里其实是可以优化空间复杂度的，就是不用数组来保存，时刻更新 i−1i-1 和 ii 所对应的各个值，然后更新和的值，具体实现可看如下代码。
注意开long long，都开就完事了，这里和朋友都栽了😭，都剩两个数据点没过，就是爆int了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n, tmp;
    ll sumzs = 0, sumfs = 0, sumzero = 0;
    ll zs = 0, fs = 0, zero = 0;
    cin >> n;
    FORU(i, 1, n)
    {
        ll cur_zs = 0, cur_fs = 0, cur_zero = 0;
        cin >> tmp;
        if (tmp > 0)
        {
            cur_zs = zs + 1;
            cur_fs = fs;
            cur_zero = zero;
        }
        else if (tmp < 0)
        {
            cur_zs = fs;
            cur_fs = zs + 1;
            cur_zero = zero;
        }
        else
            cur_zero = zero + zs + fs + 1;
        sumzs += cur_zs;
        sumfs += cur_fs;
        sumzero += cur_zero;
        zs = cur_zs;
        fs = cur_fs;
        zero = cur_zero;
    }
    cout << sumfs << ' ' << sumzero << ' ' << sumzs;
    return 0;
}

E题

题意

类似于排列组合中的取球问题：有 nn 堆，第 ii 堆有 aia_i 个相同物品，求从这 nn 堆中取出共 kk 个物品的方案数，当且仅当存在至少从一堆中取的个数不同时，才认为两种方案是不同的。
其中满足：1≤n,k≤10001\le n,k\le 1000，输出最后方案数对 998244353 取模的结果。

思路

我们用 dp[i][j]dp[i][j] 表示从前 ii 堆中选出 jj 个物品的方案数，那么它的值即等于从前 i−1i-1 堆中选出 j−mj-m 个物品，然后从第 ii 堆中选出 mm 个物品的方案数之和，则有状态转换式：(初始化 dp[i][0]=1dp[i][0]=1)

dp[i][j]=∑m=0min⁡(ai,j)dp[i−1][j−m](4)dp[i][j]=\sum_{m=0}^{\min(a_i,j)}dp[i-1][j-m]\tag{4}

其中 mm 的上限已确保数组不越界，且不会从第ii堆中选出超过其拥有的物品数。这样答案就是 dp[n][k]dp[n][k]。
但是这样就会发现本身 dp 数组是二维的，状态转移时又要累加，就是 O(nk2)O(nk^2) 的时间复杂度，哦豁，TLE 了。
这个时候我们就需要考虑优化状态转移这一步，我们发现可以用一个前缀和数组存取数组 dp[i−1]dp[i-1]，然后在状态转移的时候就直接访问 j−mj-m 到 jj 的线段和即可。这样时间复杂度就到了 O(nk)O(nk)，过！

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
int dp[1050][1050],pre[1050][1050];
int have[1050];
const int mod = 998244353;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,k;
    cin >> n >> k;
    FORU(i,1,n)
    {
        cin >> have[i];
    }
    FORU(i,0,n)
    {
        dp[i][0] = 1;
        pre[i][0] = 1;
    }
    FORU(i,1,n)
    {
        FORU(j,1,k)
        {
            pre[i - 1][j] = (pre[i - 1][j - 1] + dp[i - 1][j]) % mod;
        }
        FORU(j,1,k)
        {
            int m = min(have[i], j);
            //注意前缀和数组的使用，计算[l,r]的和用pre[r]-pre[l-1]
            if(m==j)
               dp[i][j] = dp[i][j] + pre[i - 1][j];
               //这里pre[l-1]即为0
            else
               dp[i][j] = dp[i][j] + (pre[i - 1][j] - pre[i - 1][j - m - 1]);
            dp[i][j] = (dp[i][j] + mod) % mod;
            //注意这个取模的技巧，防止出现负数
        }
    }
    cout << dp[n][k];
    return 0;
}

F题

题意

直白一点，计算勒让德多项式的系数。。。
我没大搞懂出题者的意图，是想让我们自己从罗德里格斯公式推出勒让德多项式的递推关系吗，还是说直接推出来系数的表达式？意义不明。
我是直接 wiki 的勒让德多项式的递推公式，然后场上以为是算浮点数即可，没想到是要计算分数形式，无语，好歹说一下喂(虽然样例也给了……)

思路

wiki得到：

听了讲解，原来用二项式定理就可以从罗德里格斯公式推到这个，但是依旧怎么说呢，挺无语的😓

Pn(x)=∑k=0⌊n/2⌋(−1)n(2n−2k)!2n n!(n−k)!(n−2k)(5)P_n(x)=\sum_{k=0}^{\lfloor n/2\rfloor}\frac{(-1)^n(2n-2k)!}{2^n\,n!(n-k)!(n-2k)}\tag{5}

这里⌊x⌋\lfloor x\rfloor表示向下向下取整。或者有递推关系：

Pn+1(x)=2n+1n+1xPn(x)−nn+1Pn−1(x)(6)P_{n+1}(x)=\frac{2n+1}{n+1}xP_n(x)-\frac{n}{n+1}P_{n-1}(x)\tag{6}

其中n=1,2,⋯n=1,2,\cdots，P0(x)=1P_0(x)=1，P1(x)=xP_1(x)=x。

由于本题需要计算分式，则需要分别计算分母和分子，然后再约分。
提醒，如果用式(6)迭代算的话，需要注意如果直接同分，在 23 阶的时候会出现通分后分子爆long long了，这个时候就需要先求分母最小公倍数，然后再通分。

Code

  • 利用式(5)进行计算(大概是，因为这是同学大佬的代码)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
ll gcd(ll a,ll b)
{
    return b == 0 ? a : gcd(b, a % b);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    int w = -1;
    FORU(i,0,n/2)
    {
        w *= -1;
        ll fenzi = 1, fenmu = 1;
        int cur_zi = 2 * (n - i), cur_mu = n - i;
        FORU(j,1,n)
        {
            fenzi *= cur_zi;
            fenmu *= cur_mu * 2;
            int g = gcd(fenzi, fenmu);
            fenzi /= g;
            fenmu /= g;
            cur_zi--;
            if(cur_mu>1)
                cur_mu--;
            else
            {
                if(i!=0)
                    cur_mu = i;
            }
        }
        if(n%2)
            cout << w * fenzi << '/' << fenmu << ' ' << 0 << ' ';
        else
        {
            if(i==n/2)
                cout << w * fenzi << '/' << fenmu;
            else
                cout << w * fenzi << '/' << fenmu << ' ' << 0 << ' ';
        }
    }
    cout<<endl;
    return 0;
}
  • 这是利用式(6)递推计算：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
using namespace std;
#define FORU(i, n, m) for (int i = n; i <= (int)m; ++i)
#define endl '\n'
typedef long long ll;
ll fenzi[3][35], fenmu[3][35];
ll gcd(ll a,ll b)
{
    //最大公约数
    return b == 0 ? a : gcd(b, a % b);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    fenzi[0][0] = 1;
    fenzi[1][1] = 1;
    FORU(i,0,35)
    {
        FORU(j,0,2)
        {
            fenmu[j][i] = 1;
        }
    }
    FORU(i,2,n)
    {
        FORU(j,0,i)
        {
            if(j==0)
            {
                fenzi[2][0] = -fenzi[0][0] * (i - 1);
                fenmu[2][0] = fenmu[0][0] * i;
            }
            else
            {
            	ll tg=gcd(abs(fenmu[1][j-1]),abs(fenmu[0][j]));
            	ll cur_b=fenmu[1][j-1]/tg,cur_d=fenmu[0][j]/tg;
            	fenzi[2][j]=fenzi[1][j-1]*cur_d*(2*i-1)-fenzi[0][j]*cur_b*(i-1);
            	fenmu[2][j]=cur_b*cur_d*tg*i;
                //通分时为了不爆longlong的一些无奈之举
            }
            if(fenzi[2][j]==0)
		    {
		    	fenmu[2][j]=1;
		    	continue;
			}
            ll g = gcd(abs(fenzi[2][j]), abs(fenmu[2][j]));
            fenzi[2][j] /= g;
            fenmu[2][j] /= g;
        }
        FORU(j,0,1)
        {
            //迭代，更新Pn-1和Pn-2
            memcpy(fenzi[j], fenzi[j+1], sizeof(fenzi[j]));
            memcpy(fenmu[j], fenmu[j+1], sizeof(fenmu[j]));
        }
        
    }
    for(int k=n;k>=0;k--)
    	{
   		    if(fenzi[2][k]==0)
            	cout << 0;
			else
                cout << fenzi[2][k] << "/" << fenmu[2][k];
            if(k!=0)
                cout << " ";
 		}
 		cout<<endl;
    return 0;
}

二、总结

  • 我发现我开摆了，就因为这门课免听……不是装逼，确实是感受到了自己的弱，我觉得不应该把这些归咎于我花了很多时间去学其他的，这也是一些基本功其实，哎，感觉还是没怎么规划好，希望能更有机地调节我的课内和课外。
  • 酱酱！爱7ki7ki棒棒！哈哈哈哈哈哈哈太魔性了，都给我去看派对浪客诸葛孔明，去听OP，这歌给了我十足的动力（
#算法
计算思维第二次test题解及总结
https://zongjy.github.io/2022/04/19/c33eda3b1ef5/
作者
zongjy
发布于
2022年4月19日
许可协议